Index

Welcome to my interpretation of PQC.

In the current era of emerging technologies, quantum computing poses a significant threat to our current encryption schemes. As quantum computers continue to evolve, traditional cryptographic algorithms, such as RSA and ECC, will become vulnerable to quantum attacks, compromising the confidentiality and integrity of sensitive information.

To address this challenge, NIST (National Institute of Standards and Technology) has launched a project to find candidate replacement algorithms for post-quantum cryptography. The latest information on this project can be found on their website. It is crucial to stay updated with the latest developments in PQC to ensure that our digital infrastructure remains secure.

Some additional insights on PQC:

I hope this helps! Let me know if you have any other questions or if there's anything else I can help with.

most of this information is based on the NIST PQC Round 3 Submission By Daniel et. al.

Based on my research, it appears that using the HPKE (Hybrid Public Key Encryption) standard with a post-quantum Key Exchange mechanism (KEM) is the way to go to ensure a nation-state level of security for our clients.

There are two prime candidates for the KEM: NTRU and McEliece, both of which have been selected in the third round of the NIST report. I am working on implementing both of these in order to use with hpke.js.

In terms of simplicity and time spent refining, I consider both NTRU and McEliece to be superior to the primary candidate selected by NIST. Specifically, I suggest using the following design element:

https://ntruprime.cr.yp.to/nist/ntruprime-20201007.pdf

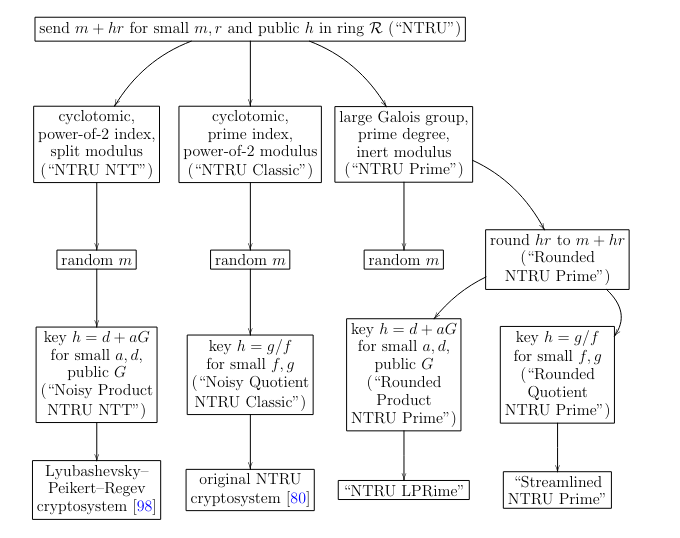
We suggest systematically using the name "NTRU" to refer to this design element and more specific names (e.g., "NTRU Classic" vs. "NTRU Prime") to refer to other designs.

It apears that we will want to use the hpke standard whit entails 2 algoithms

The first is a KEM Key Exchange mecanisim this algorithm is used to tranmit a symetric key whitch is then used for further comunication by doing this the main threat is a key exhange being compramised and thus a pqe kem is needed

There apears to be 2 prime candadates for this NTRU and mceliece

I am working on getting a working implementation of both of these to use with hpke.js in order to offer

a nation state level of security to our clients.

Both these algorithms have been selected in the 3rd round of NIST report.

I consider them both superior to the selected primary candadate on the basis of simplicity

and time spent refining.

I consider the current goal to be hpke with kem using

img.png

https://artofproblemsolving.com/wiki/index.php/Polynomial_ring

Equations:

Parameter space: (p, q, w), where p and q are prime numbers, and w is a positive integer; subject to the conditions 2p ≥ 3w and q ≥ 16w + 1; and xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].
KeyGen algorithm:
    PublicKeys = R/q and SecretKeys = Short×R/3
    Generate a random small element g ∈ R, repeat until g is invertible in R/3
    Compute 1/g in R/3
    Generate a uniform random f ∈ Short, where f is invertible in R/q
    Compute h = g/(3f ) in R/q
    Output (h, (f, 1/g)) ∈ PublicKeys × SecretKeys

Key takeaways:

Streamlined NTRU Prime has two layers: Streamlined NTRU Prime Core (PKE) and Streamlined NTRU Prime (KEM)
The parameter space for Streamlined NTRU Prime Core has certain restrictions that must be followed
The KeyGen algorithm for Streamlined NTRU Prime Core outputs an element of PublicKeys × SecretKeys and involves generating random elements and computing values based on these random elements.



Answering questions about Streamlined NTRU Prime

3.1 What are the parameters for Streamlined NTRU Prime Core?

Streamlined NTRU Prime Core has parameters (p, q, w) subject to the following restrictions:

p is a prime number;
q is a prime number;
w is a positive integer;
2p ≥ 3w;
q ≥ 16w + 1;
xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].

3.2 What is the KeyGen algorithm for Streamlined NTRU Prime Core?

The KeyGen algorithm for Streamlined NTRU Prime Core is as follows:

Define PublicKeys = R/q and SecretKeys = Short×R/3.
Generate a uniform random small element g ∈ R. Repeat this step until g is invertible in R/3.
Compute 1/g in R/3.
Generate a uniform random f ∈ Short.
Compute h = g/(3f ) in R/q.
Output (h, (f, 1/g)) ∈ PublicKeys × SecretKeys.

3.3 What is the Encrypt algorithm for Streamlined NTRU Prime Core?

The Encrypt algorithm for Streamlined NTRU Prime Core is as follows:

Input r ∈ Short and h ∈ PublicKeys.
Compute hr ∈ R/q.
Output Round(hr).

3.4 What is the Decrypt algorithm for Streamlined NTRU Prime Core?

The Decrypt algorithm for Streamlined NTRU Prime Core is as follows:

Input c ∈ Rounded and (f, v) ∈ Short × R/3.
Compute 3f c ∈ R/q.
View each coefficient of 3f c in R/q as an integer between −(q − 1)/2 and (q − 1)/2, and then reduce modulo 3, obtaining a polynomial e ∈ R/3.
Multiply e by v in R/3.
Lift ev in R/3 to a small polynomial r′ ∈ R.
Output r′ if r′ has weight w. Otherwise output (1, 1, . . . , 1, 0, 0, . . . , 0).

3.5 What is the security proof for Streamlined NTRU Prime?

The security proof for Streamlined NTRU Prime relies on the hardness of the Shortest Vector Problem (SVP) in lattices. Specifically, it is proven that if an attacker can solve the Decisional Ring-LWE problem for Streamlined NTRU Prime with probability p then there exists a polynomial-time algorithm for solving SVP in n^{O(log n)} time, where n is the degree of the polynomial ring used in the construction. This reduction assumes that the attacker has access to a certain oracle, called the “decoding oracle”, which outputs the unique closest lattice vector to a given point. This oracle is assumed to be computable in polynomial time.

Note that this security proof applies to Streamlined NTRU Prime as a whole, which includes both the inner layer (Streamlined NTRU Prime Core) and the outer layer (Streamlined NTRU Prime KEM). However, the security proof for the inner layer is simpler, and is based on the hardness of the Learning With Errors (LWE) problem in lattices. Specifically, it is proven that if an attacker can solve the Decisional LWE problem for Streamlined NTRU Prime Core with probability p then there exists a polynomial-time algorithm for solving SVP in n^{O(log n)} time, where n is the degree of the polynomial ring used in the construction. This reduction assumes that the attacker has access to

This modification helps prevent certain types of attacks, such as the "dual lattice attack," which exploit the structure of the public key to recover the secret key.

The new secret key format is (f, v, ρ), where f is the private polynomial, v = 1/g for some small g ∈ R, and ρ is a random element of Inputs. The KeyGen algorithm remains the same as in Section 2.3.1, except that the secret key now includes the ρ component. That is, after computing f and g as in KeyGen, the algorithm outputs (f, v, ρ) as the secret key.

Note that encoding and decoding algorithms for SecretKeys now include the encoding and decoding of the ρ component. Specifically, the encoding algorithm encodes (f, v, ρ) as a string (f̃, ṽ, ρ̃), where f̃ and ṽ are the encodings of f and v, respectively, and ρ̃ is the encoding of ρ. Similarly, the decoding algorithm decodes a string (f̃, ṽ, ρ̃) into (f, v, ρ).

The public key format remains the same as in Section 2.3.1. That is, it is a polynomial h = g/(3f) in R/q, encoded as a string h̃.

The encoding and decoding algorithms for PublicKeys and Ciphertexts are deterministic and invertible, as in Section 2.3.5. The encoding algorithm for Inputs simply maps each element r ∈ Inputs to its binary representation.

The HashConfirm algorithm takes an input r ∈ Inputs and a public key h ∈ PublicKeys, and outputs a string Confirm. It is implemented as a hash function that takes r and h as inputs and produces a fixed-length output.

The HashSession algorithm takes as input a bit b, an element r ∈ Inputs, a ciphertext c ∈ Ciphertexts, and a string Confirm, and outputs a string SessionKeys. It is implemented as a hash function that takes b, r, c, and Confirm as inputs and produces a

Equations:

Parameter space: (p, q, w), where p and q are prime numbers, and w is a positive integer; subject to the conditions 2p ≥ 3w and q ≥ 16w + 1; and xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].
KeyGen algorithm:
    PublicKeys = R/q and SecretKeys = Short×R/3
    Generate a random small element g ∈ R, repeat until g is invertible in R/3
    Compute 1/g in R/3
    Generate a uniform random f ∈ Short, where f is invertible in R/q
    Compute h = g/(3f ) in R/q
    Output (h, (f, 1/g)) ∈ PublicKeys × SecretKeys

Key takeaways:

Streamlined NTRU Prime has two layers: Streamlined NTRU Prime Core (PKE) and Streamlined NTRU Prime (KEM)
The parameter space for Streamlined NTRU Prime Core has certain restrictions that must be followed
The KeyGen algorithm for Streamlined NTRU Prime Core outputs an element of PublicKeys × SecretKeys and involves generating random elements and computing values based on these random elements.



Answering questions about Streamlined NTRU Prime

3.1 What are the parameters for Streamlined NTRU Prime Core?

Streamlined NTRU Prime Core has parameters (p, q, w) subject to the following restrictions:

p is a prime number;
q is a prime number;
w is a positive integer;
2p ≥ 3w;
q ≥ 16w + 1;
xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].

Shared Notation:

In the two systems, there are three common parameters:

p: a prime number
q: a prime number such that q ≥ 17 and xp − x − 1 is irreducible in the polynomial ring (Z/q)[x]
w: a positive integer such that w ≤ p

The following notation is used in both systems:

R: the ring Z[x]/(xp − x − 1)
R/3: the ring (Z/3)[x]/(xp − x − 1)
R/q: the field (Z/q)[x]/(xp − x − 1)

Additional notation and definitions for Streamlined NTRU Prime:

Short: the set of small weight-w elements of R
Rounded: the set of polynomials in R where each coefficient is in a specific set depending on q
Round: a function that maps an element in R/q to an element in Rounded
PublicKeys: the public-key space consisting of elements in R/q
SecretKeys: the secret-key space consisting of elements in Short × R/3
Inputs: the input space consisting of elements in Short
Ciphertexts: the ciphertext space consisting of elements in Rounded
Confirm: a string used in the key exchange protocol
KeyGen: a randomized algorithm that outputs an element of PublicKeys × SecretKeys
Encrypt: a public-key operation that encrypts an element in Short to an element in Ciphertexts
Decrypt: a secret-key operation that decrypts an element in Ciphertexts to an element in Short

Additional notation and definitions for NTRU LPRime:

PublicKeys′: the public-key space consisting of elements in R/q
SecretKeys′: the secret-key space consisting of elements in Short × PublicKeys × Inputs
Ciphertexts′: the ciphertext space consisting of elements in Ciphertexts × Confirm
Encap: a key-encapsulation mechanism that encapsulates a secret key and generates a ciphertext and confirm string
Decap: a key-decapsulation mechanism that decapsulates a secret key from a ciphertext and confirm string

Variable names used in Streamlined NTRU Prime:

PublicKeys: PK
SecretKeys: SK
Inputs: ρ
Ciphertexts: ct
Confirm: c

Variable names used in NTRU LPRime:

PublicKeys′: PK
SecretKeys′: SK
Inputs: not applicable
Ciphertexts′: not applicable
Confirm: not applicable

Making Noisy NTRU deterministic is more complicated than simply using Rounded Quotient NTRU, which is naturally deterministic.

A sufficiently severe weakness in Quotient NTRU would outweigh the advantages of being deterministic.

There is a claim that Product NTRU is provably at least as strong as Quotient NTRU; this claim is incorrect, as noted in [36, footnote 8] and in our submission. There is also a claim that Product NTRU attack lattices have unique short vectors while Quotient NTRU attack lattices do not; this claim is also incorrect, as noted in our round-2 submission. See Section 6.3

We caution potential users that all Product NTRU submissions, including Kyber, SABER, and NTRU LPRime, are threatened by U.S. patents 9094189 and 9246675 and by corre- sponding foreign patents. This by itself is not decisive, since the patent threats could be resolved through litigation or buyouts.

NTRU Prime was and is the only submission using a large Galois group while remaining competitive in performance with cyclotomics.

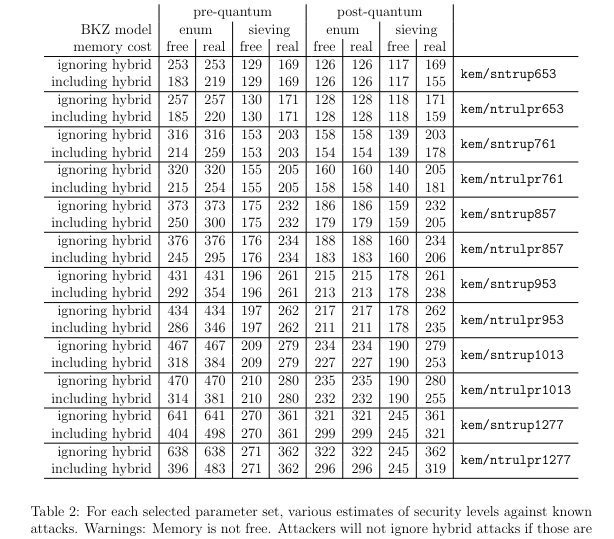
img_1.png

It seems that 761 is acceptable for tls but really for future proof we want kem/sntrup1013 paired with aes 256

https://libpqcrypto.org/install.html

https://github.com/companyzero/sntrup4591761/issues/4#issuecomment-1486039209

NIST latest report [3] nevertheless selects and prioritizes five lattice-based finalists, all using structured lattices, all using number fields with small Galois groups, specifically cyclotomics; and repeatedly expresses “confidence” in their security. This overconfidence is dangerous.

NTRU is among one of the algorithms that dose not use cyclotomics.

THey have since accepted NTRU as a finalist. No new news. all is well and good when secure it hurts nobody. If done by the people for the people :) that is what its all about.

APPEND ONLY GARBAGE jk

In a world where the threat of quantum computing looms large, most of today's security measures may become vulnerable. While we are actively exploring post-quantum encryption solutions, we must also acknowledge that the greatest risk to sensitive data often comes from the users themselves. Thus, while we strive to achieve the perfect security model, it's essential to consider the potential for human error and the need for user-friendly interfaces.

Currently, our production systems employ robust security standards, including bcrypt, AES-256, and RSA-4096, to protect data against existing threats. We are committed to staying ahead of emerging risks, which is why we continue to explore hybrid encryption methods, such as NTRU, for added security.

To address user-related risks, we impose minimal restrictions and minimize hassle to maintain standard security without compromising efficiency and productivity. We recognize that two-factor authentication (2FA) is crucial in this regard.

Our research also extends to decentralized trust and immutable storage, combining the strength of casual chains to ensure a more resilient group key management system. This approach limits the exposure time of session keys and requires daily login meetings with designated users for authentication.

Furthermore, we have implemented an authority structure with access to session keys, ensuring controlled access to sensitive data. Regular data backups provide additional protection against potential data loss.

We understand that the security landscape is continuously evolving. Therefore, we prioritize ongoing research, adaptability, and the implementation of best practices to maintain the highest security standards.

In conclusion, we believe in striking a balance between robust security measures and user-friendly experiences. By exploring cutting-edge encryption solutions, acknowledging potential user vulnerabilities, and staying vigilant against emerging threats, we can ensure the security of our systems and sensitive data.

iSales Pitch:

In today's world, the looming threat of quantum computing poses a significant challenge to our security measures. Many existing implementations are susceptible to vulnerabilities, making it crucial to explore post-quantum encryption options. However, we must also recognize that the greatest risk to sensitive data often comes from the users themselves, who may inadvertently compromise security.

To strike a balance between robust security and user-friendliness, we adhere to up-to-date standards and best practices, utilizing bcrypt, AES-256, and RSA-4096 for our production systems. We aim to minimize restrictions and hassles for users while maintaining standard security protocols, even if some of these encryption methods were previously illegal.

Moreover, we are actively working on side projects to explore the use of hybrid private key encryption. By combining well-tested and proven quantum-safe encryption, such as NTRU, with innovative key exchange mechanisms (KEMs), we can securely transfer keys.

While we acknowledge that achieving absolute security is a costly endeavor, we understand that even the most robust security model can be compromised if a single weak link, like a hijacked ad channel, grants unauthorized access to the entire system. Thus, we emphasize the importance of implementing efficient, future-proof human interfaces.

Two-factor authentication (2FA) is not to be taken lightly, as it provides an additional layer of security against potential breaches.

A significant part of our security strategy revolves around minimizing write access and reducing the attack surface by segmenting clients and controlling write access within the app. We operate under the assumption that all data in the app can be read by all users, striking a balance between complexity and security.

Our research delves into hybrid key encapsulations (HKE), where multiple KEMs such as RSA, ECC, NTRU, Falcon, etc., work in conjunction with advanced algorithms to mitigate the compromise of any single algorithm.

Furthermore, we emphasize that security is an ongoing battle. Rather than engaging in misdirection, we actively consider and implement security policies to safeguard sensitive information.

One intriguing idea we are exploring involves group-based key sharing, where multiple users combine their keys to derive a group key for symmetric encryption and decryption. To prevent compromised keys from compromising the entire group, we employ immutable storage and casual chains. We rotate session keys every 24 hours and group keys weekly, providing access only to authenticated users during designated times.

A practical example involves a group of users sharing access based on time-synced login meetings and approvals from a designated subset of users. By encrypting and syncing data locally with shared session keys, we ensure secure data handling.

To ensure security, we implement an authority structure with multiple keys, requiring a majority vote for authorization. The authority holds access to all session AES256 keys for data, which is further backed up and offloaded to internal storage.

In conclusion, our approach focuses on balancing security measures with user convenience and prioritizing ongoing research into innovative encryption techniques. By implementing up-to-date standards and best practices, exploring hybrid encryption methods, and actively considering future-proof human interfaces, we can better safeguard sensitive data and enhance overall security. User please offer a critice rebutle and any counter pointes to this. what areguments are invalid why. with refrence ChatGPT

Critical Rebuttal:

While the sales pitch presents some valid points, it also contains several misleading arguments and logical gaps. Let's break down the key issues:

Overemphasis on Quantum Computing: While it is true that quantum computing poses a potential threat to current cryptographic methods, the pitch exaggerates the immediate impact of this technology. Practical, large-scale quantum computers are still years or even decades away from realization. Current encryption standards like RSA and ECC remain secure against classical attacks, and organizations should focus on implementing strong security practices to protect against existing threats.

Reference: NIST's Post-Quantum Cryptography Standardization project [1]

Users as the Weakest Link: The pitch correctly identifies that users can introduce security vulnerabilities, but it fails to emphasize the importance of user education and awareness. Rather than accepting user mistakes as inevitable, organizations should invest in security training and enforce robust authentication methods, such as multi-factor authentication (MFA), to reduce the risk of human error.

Reference: NIST Special Publication 800-63B on Digital Identity Guidelines [2]

Post-Quantum Encryption: While exploring post-quantum encryption methods is commendable, it is crucial to clarify that current encryption standards like AES-256 and RSA-4096 remain secure against classical attacks. The implementation of post-quantum encryption should not be rushed until standardized and thoroughly vetted solutions are available.

Reference: NIST's Post-Quantum Cryptography Standardization project [1]

Hybrid Private Key Encryption (HKE): The pitch mentions the use of hybrid encryption, combining various algorithms to mitigate compromise. While hybrid encryption can offer some advantages, it also introduces complexities in implementation and potential security risks if not properly integrated and tested. Organizations must carefully assess the trade-offs before deploying such systems.

Reference: "Hybrid Encryption: Balancing Security and Performance" [3]

Minimized Permissions and Write Access: Restricting permissions and minimizing write access is a standard security practice. However, the pitch should clarify that it is just one aspect of a comprehensive security strategy and should be combined with other security measures like encryption, access controls, and regular security audits.

Reference: NIST Special Publication 800-53 on Security and Privacy Controls for Federal Information Systems and Organizations [4]

In summary, while the sales pitch touches on essential security considerations, it should avoid overhyping quantum threats and be cautious about adopting cutting-edge encryption without proper standardization and evaluation. A balanced approach to security, emphasizing user education and adopting best practices, will ultimately result in a more robust and practical security posture.

References:

https://csrc.nist.gov/projects/post-quantum-cryptography
https://doi.org/10.6028/NIST.SP.800-63b
https://link.springer.com/article/10.1007/s10207-018-0416-3
https://doi.org/10.6028/NIST.SP.800-53r5

If we continue we get HPK using bike ntru ecc rsa + we perfrom Hypercube SDitH

Whitch is a improfment of sss maybe

OK so new conclusion:

Terms KEM key exchange mekanisim Hybrid Private Key Encryption (HPKE) / HPK:

THe concept is you use many public key formats in an atempt to increase security.

this allows us the flecibility to add and remove algorithms

so for example rsa ecc ntru bike sdith etc can be used in an

sss style schem to encrypt the public key.

the intition might be im agin a high deimensional space polynomial.

we can discover this by samplein n points ehrtr p1 != p2 for all p1 and p2 in S

if we chose an group of n people we can create a group key aes 256

then we encryp it with a party key so that eack member must provide their public key to eack other to

decrypt the group key. the trick is you must provide the shard in a secure ay for this you use the same algoithm

so this is 3 layer encryption

gpriv = aes256 group seasion key for the day

let peers = server.findGroupMemeberKeys // note each peer when registered handshakes for a shared key. this key should be automaticaly rotated each day.,, maybe

pear.sign(group_shard)

let KEM(gpriv, peers, 3, ['ntru', 'ecc', 'bike_rsa_aes'])