Welcome to my interpretation of PQM.

In the current era of emerging technologies, quantum computing poses a significant threat to our current encryption schemes. As quantum computers continue to evolve, traditional cryptographic algorithms, such as RSA and ECC, will become vulnerable to quantum attacks, compromising the confidentiality and integrity of sensitive information.

To address this challenge, NIST (National Institute of Standards and Technology) has launched a project to find candidate replacement algorithms for post-quantum cryptography. The latest information on this project can be found on their website. It is crucial to stay updated with the latest developments in PQM to ensure that our digital infrastructure remains secure.

Some additional insights on PQM:

• PQM involves designing cryptographic algorithms that can resist quantum attacks, ensuring the confidentiality and integrity of data even in the presence of powerful quantum computers.
• There are several families of post-quantum cryptographic algorithms, such as lattice-based cryptography, code-based cryptography, and hash-based cryptography, each with its strengths and weaknesses.
• PQM is still a relatively new field, and many of the proposed algorithms are still under development and evaluation by experts in the field.
• It is essential to consider the efficiency and compatibility of post-quantum cryptographic algorithms with existing systems while ensuring their security.

I hope this helps! Let me know if you have any other questions or if there's anything else I can help with.

most of this information is based on the NIST PQC Round 3 Submission By Daniel et. al.

• https://ntruprime.cr.yp.to/speed.html
• https://nvlpubs.nist.gov/nistpubs/ir/2020/NIST.IR.8309.pdf
• https://en.wikipedia.org/wiki/Hybrid_cryptosystem
• https://csrc.nist.gov/Projects/post-quantum-cryptography/post-quantum-cryptography-standardization/round-3-submissions

Based on my research, it appears that using the HPKE (Hybrid Public Key Encryption) standard with a post-quantum Key Exchange mechanism (KEM) is the way to go to ensure a nation-state level of security for our clients.

There are two prime candidates for the KEM: NTRU and McEliece, both of which have been selected in the third round of the NIST report. I am working on implementing both of these in order to use with hpke.js.

In terms of simplicity and time spent refining, I consider both NTRU and McEliece to be superior to the primary candidate selected by NIST. Specifically, I suggest using the following design element:

https://ntruprime.cr.yp.to/nist/ntruprime-20201007.pdf

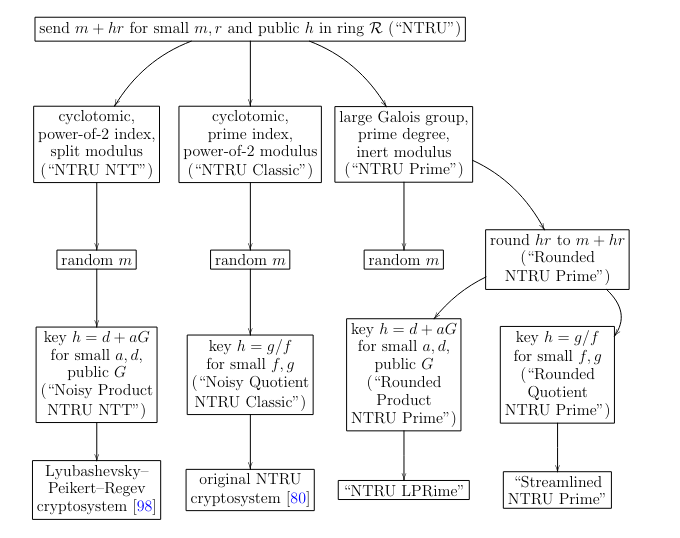
We suggest systematically using the name "NTRU" to refer to this design element and more specific names (e.g., "NTRU Classic" vs. "NTRU Prime") to refer to other designs.

It apears that we will want to use the hpke standard whit entails 2 algoithms

The first is a KEM Key Exchange mecanisim this algorithm is used to tranmit a symetric key whitch is then used for further comunication by doing this the main threat is a key exhange being compramised and thus a pqe kem is needed

There apears to be 2 prime candadates for this NTRU and mceliece

I am working on getting a working implementation of both of these to use with hpke.js in order to offer

a nation state level of security to our clients.

Both these algorithms have been selected in the 3rd round of NIST report.

I consider them both superior to the selected primary candadate on the basis of simplicity

and time spent refining.

I consider the current goal to be hpke with kem using

https://artofproblemsolving.com/wiki/index.php/Polynomial_ring

Equations:

Parameter space: (p, q, w), where p and q are prime numbers, and w is a positive integer; subject to the conditions 2p ≥ 3w and q ≥ 16w + 1; and xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].
KeyGen algorithm:
    PublicKeys = R/q and SecretKeys = Short×R/3
    Generate a random small element g ∈ R, repeat until g is invertible in R/3
    Compute 1/g in R/3
    Generate a uniform random f ∈ Short, where f is invertible in R/q
    Compute h = g/(3f ) in R/q
    Output (h, (f, 1/g)) ∈ PublicKeys × SecretKeys

Key takeaways:

Streamlined NTRU Prime has two layers: Streamlined NTRU Prime Core (PKE) and Streamlined NTRU Prime (KEM)
The parameter space for Streamlined NTRU Prime Core has certain restrictions that must be followed
The KeyGen algorithm for Streamlined NTRU Prime Core outputs an element of PublicKeys × SecretKeys and involves generating random elements and computing values based on these random elements.



Answering questions about Streamlined NTRU Prime

3.1 What are the parameters for Streamlined NTRU Prime Core?

Streamlined NTRU Prime Core has parameters (p, q, w) subject to the following restrictions:

p is a prime number;
q is a prime number;
w is a positive integer;
2p ≥ 3w;
q ≥ 16w + 1;
xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].

3.2 What is the KeyGen algorithm for Streamlined NTRU Prime Core?

The KeyGen algorithm for Streamlined NTRU Prime Core is as follows:

Define PublicKeys = R/q and SecretKeys = Short×R/3.
Generate a uniform random small element g ∈ R. Repeat this step until g is invertible in R/3.
Compute 1/g in R/3.
Generate a uniform random f ∈ Short.
Compute h = g/(3f ) in R/q.
Output (h, (f, 1/g)) ∈ PublicKeys × SecretKeys.

3.3 What is the Encrypt algorithm for Streamlined NTRU Prime Core?

The Encrypt algorithm for Streamlined NTRU Prime Core is as follows:

Input r ∈ Short and h ∈ PublicKeys.
Compute hr ∈ R/q.
Output Round(hr).

3.4 What is the Decrypt algorithm for Streamlined NTRU Prime Core?

The Decrypt algorithm for Streamlined NTRU Prime Core is as follows:

Input c ∈ Rounded and (f, v) ∈ Short × R/3.
Compute 3f c ∈ R/q.
View each coefficient of 3f c in R/q as an integer between −(q − 1)/2 and (q − 1)/2, and then reduce modulo 3, obtaining a polynomial e ∈ R/3.
Multiply e by v in R/3.
Lift ev in R/3 to a small polynomial r′ ∈ R.
Output r′ if r′ has weight w. Otherwise output (1, 1, . . . , 1, 0, 0, . . . , 0).

3.5 What is the security proof for Streamlined NTRU Prime?

The security proof for Streamlined NTRU Prime relies on the hardness of the Shortest Vector Problem (SVP) in lattices. Specifically, it is proven that if an attacker can solve the Decisional Ring-LWE problem for Streamlined NTRU Prime with probability p then there exists a polynomial-time algorithm for solving SVP in n^{O(log n)} time, where n is the degree of the polynomial ring used in the construction. This reduction assumes that the attacker has access to a certain oracle, called the “decoding oracle”, which outputs the unique closest lattice vector to a given point. This oracle is assumed to be computable in polynomial time.

Note that this security proof applies to Streamlined NTRU Prime as a whole, which includes both the inner layer (Streamlined NTRU Prime Core) and the outer layer (Streamlined NTRU Prime KEM). However, the security proof for the inner layer is simpler, and is based on the hardness of the Learning With Errors (LWE) problem in lattices. Specifically, it is proven that if an attacker can solve the Decisional LWE problem for Streamlined NTRU Prime Core with probability p then there exists a polynomial-time algorithm for solving SVP in n^{O(log n)} time, where n is the degree of the polynomial ring used in the construction. This reduction assumes that the attacker has access to

This modification helps prevent certain types of attacks, such as the "dual lattice attack," which exploit the structure of the public key to recover the secret key.

The new secret key format is (f, v, ρ), where f is the private polynomial, v = 1/g for some small g ∈ R, and ρ is a random element of Inputs. The KeyGen algorithm remains the same as in Section 2.3.1, except that the secret key now includes the ρ component. That is, after computing f and g as in KeyGen, the algorithm outputs (f, v, ρ) as the secret key.

Note that encoding and decoding algorithms for SecretKeys now include the encoding and decoding of the ρ component. Specifically, the encoding algorithm encodes (f, v, ρ) as a string (f̃, ṽ, ρ̃), where f̃ and ṽ are the encodings of f and v, respectively, and ρ̃ is the encoding of ρ. Similarly, the decoding algorithm decodes a string (f̃, ṽ, ρ̃) into (f, v, ρ).

The public key format remains the same as in Section 2.3.1. That is, it is a polynomial h = g/(3f) in R/q, encoded as a string h̃.

The encoding and decoding algorithms for PublicKeys and Ciphertexts are deterministic and invertible, as in Section 2.3.5. The encoding algorithm for Inputs simply maps each element r ∈ Inputs to its binary representation.

The HashConfirm algorithm takes an input r ∈ Inputs and a public key h ∈ PublicKeys, and outputs a string Confirm. It is implemented as a hash function that takes r and h as inputs and produces a fixed-length output.

The HashSession algorithm takes as input a bit b, an element r ∈ Inputs, a ciphertext c ∈ Ciphertexts, and a string Confirm, and outputs a string SessionKeys. It is implemented as a hash function that takes b, r, c, and Confirm as inputs and produces a

Equations:

Parameter space: (p, q, w), where p and q are prime numbers, and w is a positive integer; subject to the conditions 2p ≥ 3w and q ≥ 16w + 1; and xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].
KeyGen algorithm:
    PublicKeys = R/q and SecretKeys = Short×R/3
    Generate a random small element g ∈ R, repeat until g is invertible in R/3
    Compute 1/g in R/3
    Generate a uniform random f ∈ Short, where f is invertible in R/q
    Compute h = g/(3f ) in R/q
    Output (h, (f, 1/g)) ∈ PublicKeys × SecretKeys

Key takeaways:

Streamlined NTRU Prime has two layers: Streamlined NTRU Prime Core (PKE) and Streamlined NTRU Prime (KEM)
The parameter space for Streamlined NTRU Prime Core has certain restrictions that must be followed
The KeyGen algorithm for Streamlined NTRU Prime Core outputs an element of PublicKeys × SecretKeys and involves generating random elements and computing values based on these random elements.



Answering questions about Streamlined NTRU Prime

3.1 What are the parameters for Streamlined NTRU Prime Core?

Streamlined NTRU Prime Core has parameters (p, q, w) subject to the following restrictions:

p is a prime number;
q is a prime number;
w is a positive integer;
2p ≥ 3w;
q ≥ 16w + 1;
xp − x − 1 is irreducible in the polynomial ring (Z/q)[x].

Shared Notation:

In the two systems, there are three common parameters:

p: a prime number
q: a prime number such that q ≥ 17 and xp − x − 1 is irreducible in the polynomial ring (Z/q)[x]
w: a positive integer such that w ≤ p

The following notation is used in both systems:

R: the ring Z[x]/(xp − x − 1)
R/3: the ring (Z/3)[x]/(xp − x − 1)
R/q: the field (Z/q)[x]/(xp − x − 1)

Additional notation and definitions for Streamlined NTRU Prime:

Short: the set of small weight-w elements of R
Rounded: the set of polynomials in R where each coefficient is in a specific set depending on q
Round: a function that maps an element in R/q to an element in Rounded
PublicKeys: the public-key space consisting of elements in R/q
SecretKeys: the secret-key space consisting of elements in Short × R/3
Inputs: the input space consisting of elements in Short
Ciphertexts: the ciphertext space consisting of elements in Rounded
Confirm: a string used in the key exchange protocol
KeyGen: a randomized algorithm that outputs an element of PublicKeys × SecretKeys
Encrypt: a public-key operation that encrypts an element in Short to an element in Ciphertexts
Decrypt: a secret-key operation that decrypts an element in Ciphertexts to an element in Short

Additional notation and definitions for NTRU LPRime:

PublicKeys′: the public-key space consisting of elements in R/q
SecretKeys′: the secret-key space consisting of elements in Short × PublicKeys × Inputs
Ciphertexts′: the ciphertext space consisting of elements in Ciphertexts × Confirm
Encap: a key-encapsulation mechanism that encapsulates a secret key and generates a ciphertext and confirm string
Decap: a key-decapsulation mechanism that decapsulates a secret key from a ciphertext and confirm string

Variable names used in Streamlined NTRU Prime:

PublicKeys: PK
SecretKeys: SK
Inputs: ρ
Ciphertexts: ct
Confirm: c

Variable names used in NTRU LPRime:

PublicKeys′: PK
SecretKeys′: SK
Inputs: not applicable
Ciphertexts′: not applicable
Confirm: not applicable

Making Noisy NTRU deterministic is more complicated than simply using Rounded Quotient NTRU, which is naturally deterministic.

A sufficiently severe weakness in Quotient NTRU would outweigh the advantages of being deterministic.

There is a claim that Product NTRU is provably at least as strong as Quotient NTRU; this claim is incorrect, as noted in [36, footnote 8] and in our submission. There is also a claim that Product NTRU attack lattices have unique short vectors while Quotient NTRU attack lattices do not; this claim is also incorrect, as noted in our round-2 submission. See Section 6.3

We caution potential users that all Product NTRU submissions, including Kyber, SABER, and NTRU LPRime, are threatened by U.S. patents 9094189 and 9246675 and by corre- sponding foreign patents. This by itself is not decisive, since the patent threats could be resolved through litigation or buyouts.

NTRU Prime was and is the only submission using a large Galois group while remaining competitive in performance with cyclotomics.

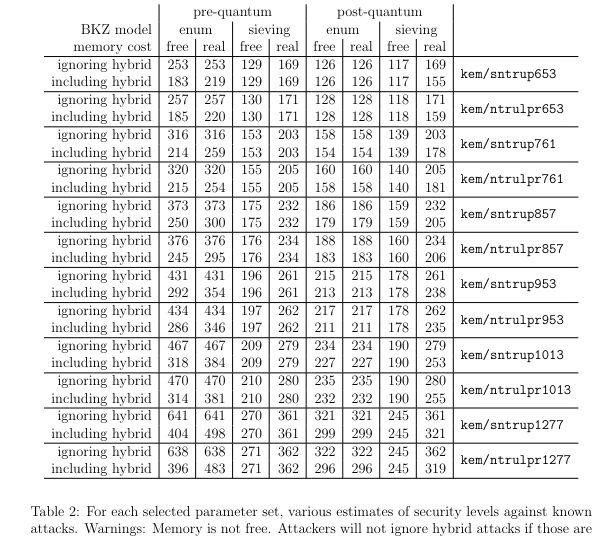
It seems that 761 is acceptable for tls but really for future proof we want kem/sntrup1013 paired with aes 256

https://libpqcrypto.org/install.html

https://github.com/companyzero/sntrup4591761/issues/4#issuecomment-1486039209

NIST latest report [3] nevertheless selects and prioritizes five lattice-based finalists, all using structured lattices, all using number fields with small Galois groups, specifically cyclotomics; and repeatedly expresses “confidence” in their security. This overconfidence is dangerous.

NTRU is among one of the algorithms that dose not use cyclotomics.

THey have since accepted NTRU as a finalist. No new news. all is well and good when secure it hurts nobody. If done by the people for the people :) that is what its all about.